Performance metrics

IQClab offers the possibility to consider various performance metrics in the IQC-analysis:

Induced 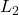$L_2$ -gain performance ( 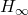$H_\infty$ -norm in case of LTI uncertainties)
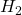$H_2$ performance (deterministic signal-based interpretation)
Generalized 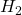$H_2$ performance (energy-to-peak performance)
Passivity performance

In addition, it is possible to consider various performance metrics related to the computation of invariant sets:

Invariant sets in the state space under the assumption that the external disturbances are bounded in energy ( $e2x$ )
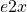Invariant sets in the performance output under the assumption that the external disturbances are bounded in energy ( $e2z$ )
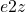Energy-to-peak gain performance ( $e2p$ )
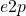Non-zero initial condition to peak gain performance ( $x2p$ )

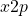If no performance metric is specified, a robust stability analysis will be carried out.

Performance metric	Description
Induced $L_2$ -gain	If selecting the induced $L_2$ -gain performance ( $H_\infty$ -norm in case of LTI uncertainties) as performance metric, then the analysis tools perform a robustness analysis, while the induced $L_2$ -gain from all specified performance inputs to all specified performance outputs is minimized. If feasible, this yields a guaranteed upper-bound, $\gamma$ , on the worst-case induced $L_2$ -gain performance for all modelled uncertainties $\Delta\in\mathbf{\Delta}$ : $\sup_{\Delta\in\mathbf{\Delta}}\\|\Delta\star M\\|<\gamma$ Note: See Section 6.1 of [1] for the details on the mathematical derivation of the corresponding performance multiplier class.
$H_2$	Similarly, if selecting the $H_2$ -norm as performance metric, then the analysis tools perform a robustness analysis, while the the $H_2$ -norm from all specified performance inputs to all specified performance outputs is minimized. If feasible, this yields a guaranteed upper-bound, $\gamma$ , on the worst-case the $H_2$ -norm performance for all modelled uncertainties $\Delta\in\mathbf{\Delta}$ : $\sup_{\Delta\in\mathbf{\Delta}}\\|\Delta\star M\\|_2<\gamma$ With $T=\Delta\star M$ , this norm is defined by $\\|T\\|_2=\sqrt{\dfrac{1}{2\pi}\mathrm{trace}\int_{-\infty}^{\infty}T(\omega) T(\omega)^d\omega.$ Notes:* – This performance metric corresponds to the deterministic signal-based interpretation. – If we let $M=\left(\begin{array}{cc}M_{11}& M_{12}\\ M_{21}& M_{22} \end{array}\right)$ with $M_{11}$ being dimension compatible with $\Delta$ , then we require $M_{12}(\infty)=0$ and $M_{22}(\infty)=0$ . -See Section 6.4 of [1] for the details on the mathematical derivation of the corresponding performance multiplier class.
Generalized $H_2$	Similar to the $H_2$ performance objective it is also possible to consider the generalized $H_2$ metric (also called the energy-to-peak gain). If feasible, this yields a guaranteed upper-bound, $\gamma$ , on the worst-case generalized $H_2$ performance for all modelled uncertainties $\Delta\in\mathbf{\Delta}$ : $\sup_{\Delta\in\mathbf{\Delta}}\\|\Delta\star M\\|_{2,\infty}<\gamma$ With $T=\Delta\star M$ , this norm is defined by $\\|T\\|_{2,\infty}=\sqrt{\dfrac{1}{2\pi}\lambda_\mathrm{max}\int_{-\infty}^{\infty}T(\omega) T(\omega)^*d\omega,$ where $\lambda_\mathrm{max}(\cdot)$ denotes the maximum eigenvalue.
Passivity	Next to the previous performance metrics, it is also possible to verify if the uncertain system $P(\Delta)=\Delta\star M$ is (strictly) input passive for all uncertainties $\Delta\in\mathbf{\Delta}$ . This means that $P(\Delta)+ P(\Delta)^\prec0$ for all $\Delta\in\mathbf{\Delta}$ . Note: See Section 6.2 of [1] for the details on the mathematical derivation of the corresponding performance multiplier class.*
$e2x$	This option allows to compute invariant sets in the state-space under the assumption that the external disturbances are bounded in energy. The option is abbreviated as $e2x$ . If feasible, this guarantees that the internal state is confined to the hyper ellipsoidal region $x(t)\in\left\{x\in\mathbb{R}^n: x^TH^{-1}x\leq\alpha^2\right\},$ for $\\|w\\|\leq\alpha$ .
$e2z$	Similarly, this option allows to compute invariant sets for the output $z$ , again under the assumption that the external disturbances $w$ are bounded in energy. The option is abbreviated as $e2z$ . If feasible, this guarantees that the output $z$ is confined to the hyper ellipsoidal region $z(t)\in\left\{z\in\mathbb{R}^n: z^TH^{-1}z\leq\alpha^2\right\},$ for $\\|w\\|\leq\alpha$ .
$e2p$	This option, which is similar to the Generalized $H_2$ performance metric, allows to compute bounds on the individual components of $z_j$ , $j\in\{1,\cdots,k\}$ . For $M_{21}(\infty)=M_{22}(\infty)=0$ being strictly proper, this option yields the peak gains $\gamma_j$ on the performance output channels $z_j$ , $j\in\{1,\cdots,k\}$ such that $\|z_j(t)\|\leq\sqrt{\gamma_j}\alpha\ \ \forall t\geq0,\ j\in\{1,\cdots,k\}.$
$x2p$	This option facilitates the computation of bounds on the peak gain of the performance output $z$ for a given non-zero initial condition $x_0\neq0$ . With $M_{21}(\infty)=0$ being strictly proper, this option computes the peak gain $\gamma$ on the performance output channel $z$ such that $\\|z(t)\\|=\\|C_2x(t)\\|\leq\gamma\\|x_0\\|\ \ \forall t\geq0$ by minimizing $\gamma$ .
Robust stability	Finally, it is also possible to verify if the uncertain system $\Delta\star M$ is stable for all $\Delta\in\mathbf{\Delta}$ . This just means that all performance channels are omitted in the analysis.

Previous page, Next page