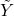The function ![]() computes the coprime factors of the stabilizable and detectable state space realization
computes the coprime factors of the stabilizable and detectable state space realization ![]() .
.
For each proper real rational transfer matrix ![]() , there exist eight transfer matrices in
, there exist eight transfer matrices in ![]() satisfying the equations:
satisfying the equations:
![]()
![]()
Let ![]() be a stabilizable and detectable realization and choose
be a stabilizable and detectable realization and choose ![]() ,
, ![]() , and
, and ![]() as:
as:
![Rendered by QuickLaTeX.com \[\begin{array}{c}R^TR=(I+D^TD)^{-1}\\ SS^T=(I+DD^T)^{-1}\\\tilde{A}=A-B (I+D^TD)^{-1}D^TC\end{array}\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-3f1ae68214cc1e31afbe8b08988f9d6c_l3.png?media=1702023987)
![]()
Define the state feedback and observer gains ![]() and
and ![]() as:
as:
![]()
![Rendered by QuickLaTeX.com \[\begin{array}{c} T_\mathrm{l}=\left(\begin{array}{cc} \tilde{X}&-\tilde{Y}\\-\tilde{N}&\tilde{M} \end{array}\right)= \left[\begin{array}{c|cc}A+HC&-(B+HD)&H\\ \hline R^{-1}F& R^{-1} &0\\ SC&-SD&S\end{array}\right]\\T_\mathrm{r}=\left(\begin{array}{cc}M&Y\\N&X\end{array}\right)= \left[\begin{array}{c|cc}A+BF&BR&-HS^{-1}\\ \hline F&R&0\\ C+DF&DR&D^{-1}\end{array}\right]\end{array}\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-7ceb85959ff939dc1bbcb4682cf39a9a_l3.png?media=1702023987)
As output the function provides the structures ![]() and
and ![]() with the realizations of respectively:
with the realizations of respectively:
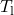 ,
, 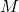 ,
, 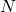 ,
,  ,
, 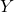
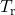 ,
, 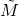 ,
, 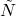 ,
, 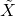 ,
,