The function ![]() computes the
computes the ![]() balanced realization for the stable system
balanced realization for the stable system ![]() .
.
As output you obtain the ![]() balanced realization
balanced realization
![]()
The balancing proceeds as follows:
- First, the function computes the
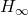 -norm,
-norm, 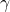 of the stable system
of the stable system 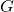 .
. - With
compute the solutions of the algebraic Riccati (ARE) equations![Rendered by QuickLaTeX.com \[\begin{array}{c}D_h^TD_h=-\left(\frac{1}{\gamma}D^TD-\gamma I\right)\prec0\\D_cD_c^T=-\left(\frac{1}{\gamma}DD^T-\gamma I\right)\prec0\end{array}\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-c1867a771e0f7753209ef8f1a4c579d9_l3.png?media=1702023987)
which are guaranteed to have a solution![Rendered by QuickLaTeX.com \[\begin{array}{c}XA+A^TX+\frac{1}{\gamma}C^TC+\left(\bullet}\right)^T\!\!\left(D_h^TD_h-\gamma I\right)^{-1}\!\!\left(XB+\frac{1}{\gamma}C^TD\right)\\AY+YA^T+\frac{1}{\gamma}BB^T+\left(\bullet\right)^T\!\!\left(D_cD_c^T-\gamma I\right)^{-1}\!\!\left(XC^T+\frac{1}{\gamma}BD^T\right)\end{array},\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-87d9ecf2a7e749628b41091bbf963fce_l3.png?media=1702023987)
 and
and 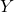 respectively.
respectively. - These solutions can now be used to perform a standard balancing.
