The function ![]() constructs the extended Lyapunov matrix
constructs the extended Lyapunov matrix ![]() in various fashions. Given the symmetric and nonsignular matrices
in various fashions. Given the symmetric and nonsignular matrices ![]() and
and ![]() (perturb if necessary), the function can be extended the Lyapunov function
(perturb if necessary), the function can be extended the Lyapunov function ![]() such that:
such that:
| Types | Description |
| 1-6 | For the coupling condition construct the extended Lyapunov matrix |
| 7-12 | For the coupling condition construct the extended Lyapunov matrix |
| 13-15 | For the coupling condition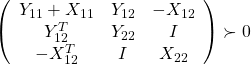 with construct the extended Lyapunov matrix |
The different types are constructed as follows
| Type | Description |
| 1 | |
| 2 | |
| 3 | If If |
| 4 | |
| 5 | If 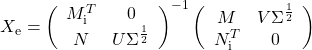 If 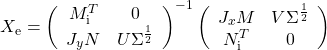 |
| 6 | If If |
| 7 | |
| 8 | |
| 9 | If If |
| 10 | |
| 11 | If 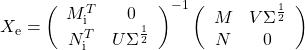 If 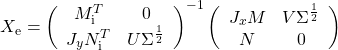 |
| 12 | If If |
| 13 | |
| 14 | |
| 15 | |

![Rendered by QuickLaTeX.com \[X_\mathrm{e}=\left(\begin{array}{ccc}X_{11}&X_{12}&X_{13}\\ X_{12}^T&X_{22}&X_{23}\\ X_{13}^T&X_{23}^T&X_{33} \end{array}\right)\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-8c291ef9d2a45b6ebd340f6a9c4b2d3c_l3.png?media=1702023987)