fSquare

The function [\hat{\Psi},\hat{M},Z,R]=fSquare(\Psi_1,\Psi_2,M,options) computes the upper-triangular outer factors of the IQC-multiplier \left(\begin{array}{cc}\Psi_1&\Psi_2\end{array}\right)^*M \left(\begin{array}{cc}\Psi_1&\Psi_2\end{array}\right), where:

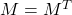  • M=M^T is a symmetric matrix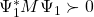
  • \Psi_1^*M\Psi_1\succ0
  • \Psi_2^*M\Psi_2-\left(\Psi_1^*M\Psi_2\right)^*\left(\Psi_1^*M\Psi_2\right)^{-1}\left(\Psi_1^*M\Psi_2\right)\prec0

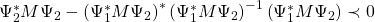
Here \Psi_i=ss(A_i,B_i,C_i,D_i), i\in\{1,2\} are assumed to admit minimal realizations.

As output, in case of options=’eq’, you obtain:

  1. The factorization

        \[\left(\begin{array}{cc}\Psi_1&\Psi_2\end{array}\right)^*M\left(\begin{array}{cc}\Psi_1&\Psi_2\end{array}\right)=\hat{\Psi}\hat{M}\hat{\Psi}=\]

        \[= \left(\begin{array}{cc}\hat{\Psi}_1&\hat{\Psi}_3\\0&\hat{\Psi}_2\end{array}\right)^*\left(\begin{array}{cc}I&0\\0&-I\end{array}\right)\left(\begin{array}{cc}\hat{\Psi}_1&\hat{\Psi}_3\\0&\hat{\Psi}_2\end{array}\right),\]

    where \hat{\Psi}_1 \hat{\Psi}_2, \hat{\Psi}_3, \hat{\Psi}_1^{-*}, \hat{\Psi}_2^{-*}\in RH_\infty.
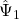
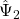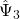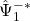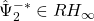  2. The matrix

        \[\hat{M}=\left(\begin{array}{cc}I&0\\0&-I\end{array}\right)\]

  3. The controllable realization

        \[\left(\begin{array}{cc}\hat{\Psi}_1&\hat{\Psi}_3\\0&\hat{\Psi}_2\end{array}\right)=\left[\begin{array}{cc|cc}A_1&0&B_1&0\\0&A_{2c}&0&B_{2c}\\ \hline \hat{C}_1&\hat{C}_{3c}&\hat{D}_1&\hat{D}_{3c}\\0&C_{2c}&0&D_{2c}\end{array}\right].\]

  4. The matrix 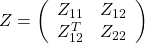Z=\left(\begin{array}{cc}Z_{11}&Z_{12}\\Z_{12}^T&Z_{22}\end{array}\right) that certifies the linear matrix equation

        \[\left(\bullet\right)^T\left(\begin{array}{cc|cc|cc|c}0&0&Z_{11}&Z_{12}&0&0&0\\0&0&Z_{12}^T&Z_{22}&0&0&0\\ \hline Z_{11}&Z_{12}&0&0&0&0&0\\Z_{12}^T&Z_{22}&0&0&0&0&0\\ \hline 0&0&0&0&I&0&0\\0&0&0&0&0&-I&0\\ \hline 0&0&0&0&0&0&-M\end{array}\right)\times\]

        \[\times\left(\begin{array}{cc|cc}I&0&0&0\\0&I&0&0\\ \hline A_1&0&B_1&0\\0&A_{2c}&0&B_{2c}\\ \hline \hat{C}_1&\hat{C}_{3c}&\hat{D}_1&\hat{D}_{3c}\\0&C_{2c}&0&D_{2c}\\ \hline C_1&(0\ C_2)&D_1&D_2\end{array}\right)=0\]

  5. The realization matrices (as a structure R): \hat{C}_1, \hat{D}_1, \hat{D}_{1i}=\hat{D}_1^{-1}, A_{2c}, B_{2c}, C_{2c}, D_{2c}, D_{2ci}=D_{2c}^{-1}, C_{3c}, D_{3c}.

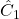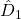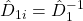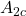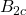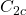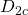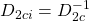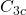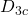If options=’ineq’, the factorization is performed such that:

    \[\left(\begin{array}{cc}\Psi_1&\Psi_2\end{array}\right)^*M\left(\begin{array}{cc}\Psi_1&\Psi_2\end{array}\right)\prec\hat{\Psi}\hat{M}\hat{\Psi}=\]

    \[= \left(\begin{array}{cc}\hat{\Psi}_1&\hat{\Psi}_3\\0&\hat{\Psi}_2\end{array}\right)^*\left(\begin{array}{cc}I&0\\0&-I\end{array}\right)\left(\begin{array}{cc}\hat{\Psi}_1&\hat{\Psi}_3\\0&\hat{\Psi}_2\end{array}\right)\]

and

    \[\left(\bullet\right)^T\left(\begin{array}{cc|cc|cc|c}0&0&Z_{11}&Z_{12}&0&0&0\\0&0&Z_{12}^T&Z_{22}&0&0&0\\ \hline Z_{11}&Z_{12}&0&0&0&0&0\\Z_{12}^T&Z_{22}&0&0&0&0&0\\ \hline 0&0&0&0&I&0&0\\0&0&0&0&0&-I&0\\ \hline 0&0&0&0&0&0&-M\end{array}\right)\times\]

    \[\times\left(\begin{array}{cc|cc}I&0&0&0\\0&I&0&0\\ \hline A_1&0&B_1&0\\0&A_{2c}&0&B_{2c}\\ \hline \hat{C}_1&\hat{C}_{3c}&\hat{D}_1&\hat{D}_{3c}\\0&C_{2c}&0&D_{2c}\\ \hline C_1&(0\ C_2)&D_1&D_2\end{array}\right)\prec0.\]

Previous page