Implementing the Bounded Real Lemma

The file Demo_011.m is found in IQClab’s folder demos; it demonstrates how to implement a new LMI problem. More specifically, we show how to implement the Bounded-Real Lemma and demonstrate how we can check if a random LTI system is stable and what the corresponding $H_\infty$ norm is.

To this end, let us consider the LTI system $G=ss(A,B,C,D)$ , and assume that the pair $(A,B)$ is controllable. This system is stable and has an $H_\infty$ -norm smaller than $\gamma$ if and only if there exists a positive definite solution $X\succ0$ for which the following matrix inequality is feasible:

$\left(\!\!\begin{array}{cc}I&0\\A&B\\C&D\\0&I\end{array}\!\!\right)^{\!T}\!\!\left(\!\!\begin{array}{cccc} 0&X&0&0\\X&0&0&0\\0&0&\gamma^{-1}I&0\\0&0&0&-\gamma I\end{array}\!\!\right)\!\! \left(\!\!\begin{array}{cc} I&0\\A&B\\C&D\\0&I\end{array}\!\!\right)\!\prec \!0$ .

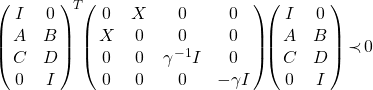This can be easily written as a genuine LMI by applying the Schur complement. This yields:

$\left(\!\!\begin{array}{ccc}I&0&0\\A&B&0\\0&I&0\\0&0&I\end{array}\!\!\right)^{\!T} \!\! \left(\!\!\begin{array}{cccc}0&X&0&0\\X&0&0&0\\0&0&-\gamma I&0\\0&0&0&-\gamma I\end{array}\!\!\right)\!\! \left(\!\!\begin{array}{ccc} I&0&0\\A&B&0\\0&I&0\\0&0&I\end{array}\!\!\right)\!\prec\!-\left(\!\!\begin{array}{ccc}0&0&C^T\\0&0&D^T\\C&D&0\end{array}\!\!\right)$ .

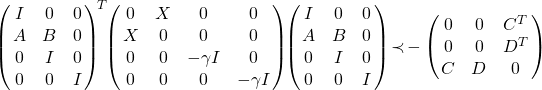This LMI can be easily implemented as follows:

% Define random LTI system with n states
n       = 10;
G       = rss(n,1,2);
[no,ni] = size(G);

% Define IQC-LMI problem
prob  = iqcprob;

% Define LMI variables
X     = iqcvar(prob,[n,n],'symmetric');
gamma = iqcvar(prob,[1,1],'full');

% Define LMI
P     = blkdiag(oblkdiag(X),-gamma*eye(no+ni));
A     = [eye(n),zeros(n,no+ni);G.a,G.b,zeros(n,no);...
        zeros(ni+no,n),eye(no+ni)];
B     = fHe([zeros(n+ni,n+no+ni);-[G.c,G.d,zeros(no)]]);

prob  = iqclmi(prob,P,-1,B,A);
prob  = iqclmi(prob,X,1);

% Solve IQC-LMI problem
prob  = iqcsolve(prob,gamma);

% Check solution
P     = iqcdec2mat(prob,P);
X     = iqcdec2mat(prob,X);
gamma = iqcdec2mat(prob,gamma);

disp('Check if the main LMI is negative definite:');
disp(eig(A'*P*A-B));
disp('Check if X is positive definite');
disp(eig(X));
disp('The computed bound on the H-infinity norm is:');
disp(gamma);