In this section it is demonstrated how to create a static diagonally repeated LTI uncertainty block. To do so, suppose that this uncertainty has the following properties:
- name: ‘delta’
- Uncertainty block consisting of two parametric uncertainties
 and
and 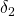
- bounds:
![Rendered by QuickLaTeX.com \delta_1\in[-1,1]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-6df548fdeecebbca619752484cf9738e_l3.png?media=1702023987) ,
, ![Rendered by QuickLaTeX.com \delta_2\in[-1,1]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-d77e46ebba1eba28f4cd385696b71327_l3.png?media=1702023987)
- number of repetitions: 2 and 6 times for
 and
and 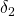 respectively
respectively - Input channels of
 connecting the uncertainty block:
connecting the uncertainty block: 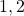 for
for  and
and  for the
for the 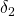
- Outputs channels of
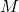 connecting the uncertainty block:
connecting the uncertainty block: 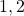 for
for  and
and  for
for 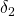
This uncertainty can be created as follows:
delta = iqcdelta('delta','InputChannel',{[1:2],[3:8]},'OutputChannel',{[1:2],[3:8]},'Bounds',{[-1,1],[-1,1]});
Alternatively, though in a bit more cumbersome way, you can also specify each block independently and then combine them with blkdiag as follows:
delta1 = iqcdelta('delta1','InputChannel',1:2,'OutputChannel',1:2,'Bounds',[-1,1]);
delta2 = iqcdelta('delta2','InputChannel',3:8,'OutputChannel',3:8,'Bounds',[-1,1]);
delta = blkdiag('delta',delta1,delta2);
In a next step, you have to assign an IQC-multiplier. The appropriate class for this is called ultis (for details see here).
Now suppose you want the basis function have the following properties:
- Length: 2 (this corresponds to a McMillan degree of 1)
- Pole location: -10
This can be specified as:
delta = iqcassign(delta,'ultis','Length',2,'PoleLocation',-10);
If you want to trade of computational complexity versus performance, it is also possible to specify the length and the pole location for each parametric uncertainty separately as:
This can be specified as:
delta = iqcassign(delta,'ultis','Length',[2,1],'PoleLocation',[-10,-1]);
