In this section it is demonstrated how to create a full-block LTV parametric uncertainty block. To do so, suppose that this uncertainty has the following properties:
- name: ‘Delta’
- Uncertainty block
 is defined by the map
is defined by the map
with![Rendered by QuickLaTeX.com \[\Delta(\delta)\!=\!\left(\!\!\begin{array}{cc}1&0\\0&1\end{array}\!\!\right)\delta_1\!+\!\left(\!\!\begin{array}{cc}1&1\\0&0\end{array}\!\!\right)\delta_2\!+\!\left(\!\!\begin{array}{cc}0&1\\1&0\end{array}\!\!\right)\delta_3\!+\!\left(\!\!\begin{array}{cc}1&0\\1&0\end{array}\!\!\right)\delta_4\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-ea530ebf8be77097c7b980ee764c8fa4_l3.png?media=1702023987)

- bounds:
![Rendered by QuickLaTeX.com \delta_i\in[-0.1,0.1]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-ae208a5758e46c7c801e172e951fe9d3_l3.png?media=1702023987) ,
, 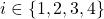
- Input channels of
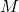 connecting the uncertainty block:
connecting the uncertainty block: 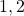
- Outputs channels of
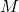 connecting the uncertainty block:
connecting the uncertainty block: 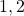
This uncertainty can be created as follows:
H{1} = [1,0;0,1];
H{2} = [1,1;0,0];
H{3} = [0,1;1,0];
H{4} = [1,0;1,0];
La = polydec(pvec('box',0.1*[-1,1;-1,1;-1,1;-1,1]))';
Delta = iqcdelta('Delta','InputChannel',1:2,'OutputChannel',1:2,'TimeInvTimeVar','TV','Structure','FB', 'UncertaintyMap',H,'Polytope',La);
In a next step, you have to assign an IQC-multiplier. The appropriate class for this is called ultv (for details see here).
For this multiplier you have to choose the type of relaxation. At the moment you can choose between four options. In this example, we wish to consider the convex hull relaxation, which can be specified as (though a typical analysis would start with the less computationally demanding ‘DG’ option):
Delta = iqcassign(Delta,'ultv','RelaxationType','CH');
