IQC-analysis for LTI systems

In many applications, the uncertainties may be confined to the subclass of LTI parametric and dynamic uncertainties. In such cases, it may be sufficient to just perform a $\mu$ -analysis using the available routines in the MATLAB’s Robust Control Toolbox (e.g., robustab, wcgain).

Then one would define the uncertain plant as an LFT object (being defined by an LTI plant $M$ and a structured uncertainty block $\Delta$ consisting of LTI parametric (ureal) and/or dynamic (ultidyn) uncertainties).

However, sometimes it still may be useful to perform a complementary IQC-analysis. In such cases, IQClab can perform an IQC-analysis without the need for setting up the analysis problem in IQClab (using the routines iqcdelta and iqcassign). This can be done by means of the function mu2iqcanalysis, which provides an easy interface that simplifies the usage of the tools.

The function can be called as follows:

$[ga,info] = mu2iqcanalysis(uobject,order,varargin).$

Here

uobject is the uncertain stable continuous- or discrete time plant (LFT)
order is the only necessary additional input, being an integer 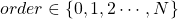$order\in\{0,1,2\cdots,N\}$ . This value corresponds to the McMillan degree of the basis function $\Psi$ , which equals its length plus 1. Note here that a higher order come at the cost of more computational load.
The option varargin allows specifying additional properties in the IQC-analysis similar to the function iqcanalysis. This proceeds specifying the properties in pairs as discussed in the following table.

Property	Description
Parser	It is possible to select either one of the following parsers: 1. ‘LMIlab’ (default) 2. ‘Yalmip’
Solver	If selecting LMIlab, the Matlab solvers mincx, and feasb are used to solve the minimization and feasibility problem respectively. On the other hand, if using Yalmip, you can consider various solvers, such as e.g., mosek, sdpt3, sedumi, etc. The reader is referred to https://yalmip.github.io/allsolvers/ for an overview of solvers that are supported.
SolChk	‘SolChk’ allows to verify whether an obtained LMI solution is indeed feasible (default = ‘off’)

Note: In case you would like to have more freedom to trade-off accuracy with computational complexity, it is also possible to consider the function fLFTdata. Click here for further details.