IQClab also provides the option to perform Robust controller synthesis with general dynamic multipliers. This yields controllers that are robust with respect to the modelled uncertainties.
Note: It is assumed that the user is acquainted with the IQC synthesis literature. The reader is referred to [8], [9] and references therein for further information.
The algorithm considered here is identical to the one presented in [8] , which considers the problem of nominal controller synthesis with unstable weights that have no poles on the imaginary axis [8], [9]. This problem turns out to be very useful in a ![]() -like synthesis algorithm for the systematic design of robust controllers with a general linear fractional dependence on the uncertainties. Such algorithms all rely on a suitable factorization of the involved multipliers, which frequently causes numerical ill-conditioning in computations. The present algorithm avoids any such factorizations. If compared to the existing approaches, this leads to a drastically simplified synthesis algorithm for the systematic design of robust controllers based on general dynamic IQC-multipliers.
-like synthesis algorithm for the systematic design of robust controllers with a general linear fractional dependence on the uncertainties. Such algorithms all rely on a suitable factorization of the involved multipliers, which frequently causes numerical ill-conditioning in computations. The present algorithm avoids any such factorizations. If compared to the existing approaches, this leads to a drastically simplified synthesis algorithm for the systematic design of robust controllers based on general dynamic IQC-multipliers.
We consider the system interconnection shown in the following figure.
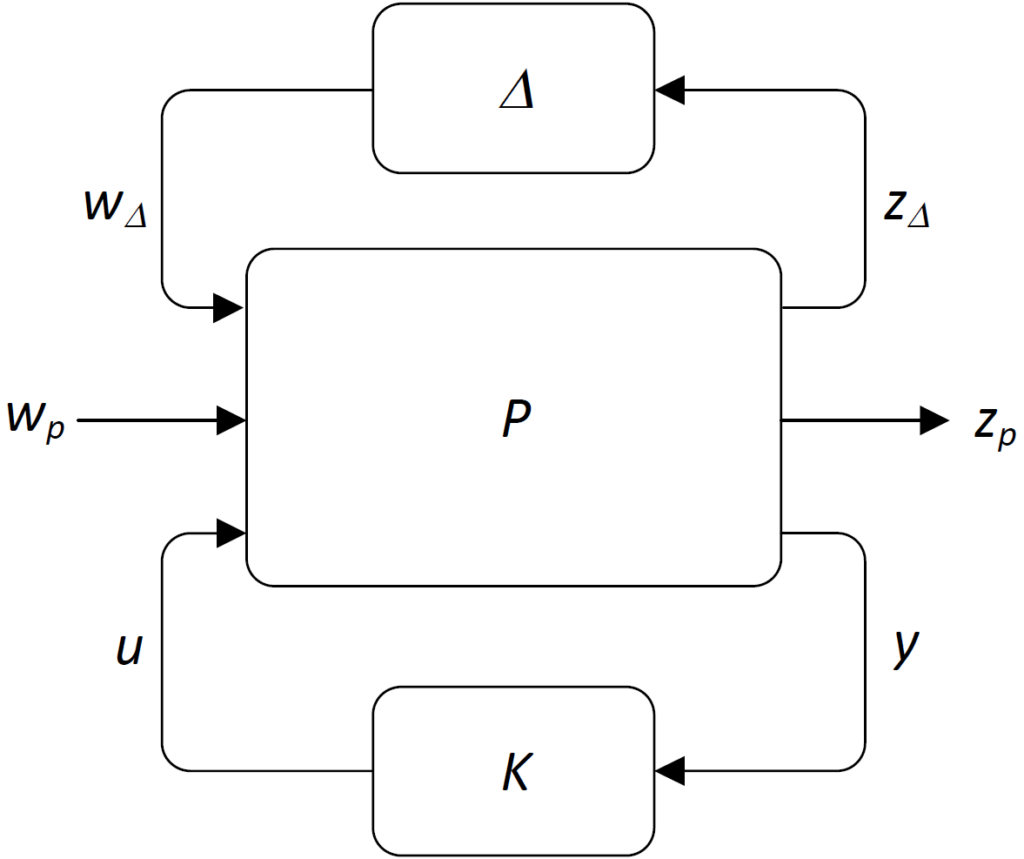
Here:
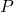 is the generalized plant (i.e., it is assumed that the disturbance and performance weights are already incorporated in the plant)
is the generalized plant (i.e., it is assumed that the disturbance and performance weights are already incorporated in the plant) is the uncertainty block, which is assumed to have a block diagonal structure
is the uncertainty block, which is assumed to have a block diagonal structure  . The properties of the individual blocks should be compatible with those from the class iqcdelta (see details here)
. The properties of the individual blocks should be compatible with those from the class iqcdelta (see details here)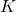 is the to-be-designed robust controller
is the to-be-designed robust controller- the in- and output channels are given by
 is the performance channel
is the performance channel
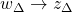 is the uncertainty channel
is the uncertainty channel is the control channel
is the control channel
Some characteristics of the algorithm are:
- The algorithms performs a synthesis with the aim to obtain a robust controller,
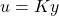 , which, for all
, which, for all  , stabilizes the plant
, stabilizes the plant  and renders the induced
and renders the induced  -gain on the performance channel
-gain on the performance channel  less than
less than 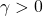 .
. - The
 -block is compatible with the class iqcdelta (see details here)
-block is compatible with the class iqcdelta (see details here) - The algorithms imposes the following induced
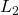 norm constraint on the performance channel
norm constraint on the performance channel  :
:
Here![Rendered by QuickLaTeX.com \[\int_0^{\infty}\left(\begin{array}{c}z_\mathrm{p}(t)\\w_\mathrm{p}(t)\end{array}\right)^T\left(\begin{array}{cc}\frac{1}{\gamma}I&0\\0&-\gamma I\end{array}\right)\left(\begin{array}{c}z_\mathrm{p}(t)\\w_\mathrm{p}(t)\end{array}\right)dt\geq0\ \ \forall t\geq0.\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-0d30465dd65d5ef7c70e1c61d8bcf744_l3.png?media=1702023987)
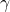 is the to-be-minimized induced
is the to-be-minimized induced 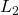 -gain.
-gain. - The algorithm relies on an iteration between performing nominal (weighted) controller syntheses and IQC robustness analyses. This is similar to the
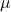 -synthesis approach. The essential different is that the present algorithm allows to consider general dynamic IQC multipliers and does not rely on any factorization of the multipliers.
-synthesis approach. The essential different is that the present algorithm allows to consider general dynamic IQC multipliers and does not rely on any factorization of the multipliers.
The algorithm proceeds as follows:
- Initialization (iteration step
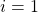 )
)
- Design a standard
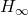 controller
controller 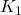 with
with 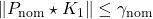
- Construct the closed-loop system
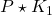 and perform an IQC-analysis. This yields the upper-bound
and perform an IQC-analysis. This yields the upper-bound 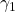 with
with 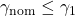 and
and 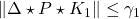 for all
for all 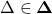 .
.
- Design a standard
- Iteration (step
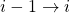 for
for 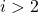 )
)
- With the multiplier
 from the IQC-analysis for
from the IQC-analysis for 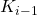 , design a new controller
, design a new controller 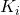 . Minimization yields the bound
. Minimization yields the bound 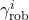 with
with 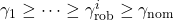 and
and 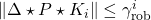 for all
for all 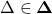 .
. - Build the closed-loop system
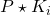 and perform an IQC-analysis. This yields the bound
and perform an IQC-analysis. This yields the bound 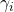 with
with 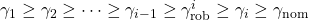 and
and 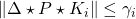 for all
for all 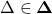 .
. - Terminate if
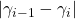 is small.
is small.
- With the multiplier
The iteration yields the controllers ![]() and worst-case induced
and worst-case induced ![]() -gains
-gains ![]() , which guarantee
, which guarantee ![]() to be stable and which render
to be stable and which render ![]() for all
for all ![]() .
.
Usage:
If feasible, the algorithms returns for each iteration:
- The stabilizing controllers
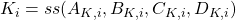 .
. - The (guaranteed) induced
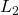 -gain,
-gain, 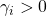 on the performance channel
on the performance channel  of the closed-loop system
of the closed-loop system 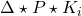 .
.
The inputs should be provided as follows:
- The LTI plant
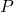 is assumed to admit the following state space description
is assumed to admit the following state space description
where![Rendered by QuickLaTeX.com \[\left(\!\!\!\begin{array}{c}z_\Delta\\z_\mathrm{p}\\y\end{array}\!\!\!\right)\!=\!\left[\!\!\begin{array}{c|ccc}A&B_\Delta&B_\mathrm{p}&B_u\\ \hline C_\Delta&D_{\Delta\Delta}&D_{\Delta\mathrm{p}}&D_{\Delta u}\\C_\mathrm{p}&D_{\mathrm{p}\Delta}&D_\mathrm{pp}&D_{\mathrm{p}u}\\C_y&D_{y\Delta}&D_{y\mathrm{p}}&D_{yu}\end{array}\!\!\right]\!\!\!\left(\!\!\begin{array}{c}w_\Delta\\w_\mathrm{p}\\u\end{array}\!\!\!\right),\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-0b253f8bc5afd713372b7dd25457cbcf_l3.png?media=1702023987)
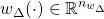 and
and  are the uncertainty and disturbance inputs
are the uncertainty and disturbance inputs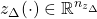 and
and 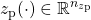 are the uncertainty and performance outputs
are the uncertainty and performance outputs
 is the control input
is the control input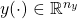 is the measurement output
is the measurement output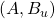 is stabilizable and
is stabilizable and  is detectable
is detectable
- The uncertainty block
 is an iqcdelta object, to which IQC-multipliers have been assigned with iqcassign (see details here).
is an iqcdelta object, to which IQC-multipliers have been assigned with iqcassign (see details here). - The plant input and output dimension data
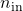 and
and 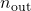 must be specified as follows:
must be specified as follows:
- The last input, options, is a structure with various options as summarized in the following table.
| Options | Description |
| options.maxiter | This option defines the maximum number of iterations (default = 10). |
| options.subopt | If chosen larger than 1, the algorithm computes a suboptimal solution The default value is 1.05. |
| options.condnr | If chosen larger than 1, the algorithm computes a suboptimal solution by maximizing The default value is 1. |
| options.constants | options.constants= The constants are associated with the following LMI constraints – – – The default value is |
| options.gmax | This option specifies the maximum induced The default value is 1000. |
| options.Pi11pos | To improve the conditioning of the IQC-multiplier sub-block To do so, one can specify ‘ Pi11pos’ (default = 0). Note: |
| options.Parser | The option options.Parser specifies which parser is used: – options.Parser=’LMIlab’ – options.Parser=’Yalmip’ The default options is ‘LMIlab’. |
| options.Solver | The option options.Solver specifies which solver is used when considering Yalmip as parser. See https://yalmip.github.io/ for further info. The default solver is ‘mincx’. |
| options.FeasbRad | This option allows setting the feasibility radius of the optimization problem (see MATLAB → help → mincx for further details). The default value is 1e9. |
| options.Terminate | This option can be used to change the LMI solver options (see MATLAB → help → mincx for further details). The default value is 0. |
| options.RelAcc | This option can be used to change the LMI solver options (see MATLAB → help → mincx for further details). The default value is 1e-4. |

![Rendered by QuickLaTeX.com \[\left(\!\!\begin{array}{ccc}Y_{11}+X_{11}&Y_{12}&-X_{12}\\Y_{12}^T&Y_{22}&I\\-X_{12}^T&I&X_{22}\end{array} \!\!\right)\!\succ\!c_1I\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-fb46c40360bc7b1115625c791cbb3918_l3.png?media=1702023987)