The file Demo_004.m is found in IQClab’s folder demos. This demo performs an IQC-robustness analysis for an uncertain plant that is affected by arbitrarily fast time-varying parametric uncertainties. Here it is possible to vary several inputs:
- The uncertainty block:
- Two LTV parametric uncertainties that are diagonally repeated once, or
- Four LTV parametric uncertainties packed in a full
 delta-block
delta-block
- Performance metric:
- Induced
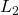 -gain
-gain 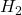 -norm
-norm- Robust stability test
- Induced
The uncertain system is given by ![]() with the open-loop LTI plant
with the open-loop LTI plant ![]() , where
, where
![]() ,
, ![]() ,
, 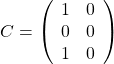 ,
,  ,
,
while:
 for Option 2.1 and Option 2.3,
for Option 2.1 and Option 2.3, for Option 2.2.
for Option 2.2.
On the other hand, the uncertainty block is defined by:
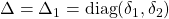 with
with ![Rendered by QuickLaTeX.com \delta_i\in[-\alpha,\alpha]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-e54b54a6519dc8c0a782847c1dafae7b_l3.png?media=1702023987) ,
,  , for Option 1.1, or
, for Option 1.1, or for Option 1.2, where
for Option 1.2, where  ,
,  ,
,  ,
,  , and
, and ![Rendered by QuickLaTeX.com \delta_i\in[-\alpha,\alpha]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-e54b54a6519dc8c0a782847c1dafae7b_l3.png?media=1702023987) ,
, 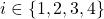 .
.
The demo file Demo_004.m allows to run an IQC-analysis for various values of ![]() and different relaxation schemes. Within the file one can change the inputs mentioned above. For illustration purposes, the following code specifies an IQC-analysis for the uncertain plant
and different relaxation schemes. Within the file one can change the inputs mentioned above. For illustration purposes, the following code specifies an IQC-analysis for the uncertain plant ![]() ,
, ![]() ,
, ![]() , and the induced
, and the induced ![]() -gain as performance metric. In addition, the following parameters are considered:
-gain as performance metric. In addition, the following parameters are considered:
- Relaxation type: ‘CH’
- Solution check: ‘on’
- Enforce strictness of the LMIs:

% Define uncertain plant
M = ss([-2,-3;1,1],[1,0,1;0,0,0],[1,0;0,0;1,0],[1,-2,0;1,-1,1;0,1,0]);
% Define uncertainty block
H{1} = [1,0;0,1]; H{2} = [1,1;0,0]; H{3} = [0,1;1,0]; H{4} = [1,0;1,0];
La = polydec(pvec('box',0.1*[-1,1;-1,1;-1,1;-1,1]))';
de = iqcdelta('de','InputChannel',1:2,'OutputChannel' ,1:2,'Structure','FB','UncertaintyMap',H,'Polytope',La,'TimeInvTimeVar','TV');
% Assign IQC-multiplier to uncertainty block
de = iqcassign(de,'ultv','RelaxationType','CH');
% Define performance block
pe = iqcdelta('pe','ChannelClass','P','InputChannel', 3,'OutputChannel',3,'PerfMetric','L2');
% Perform IQC-analysis
prob = iqcanalysis(M,{de,pe},'SolChk','on','eps',1e-8);
To continue, if running the IQC-analysis in Demo_004.m for
 (Option 1.2)
(Option 1.2)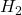 -gain performance (Option 3.2)
-gain performance (Option 3.2)
you obtain the worst-case ![]() -norm for increasing values of
-norm for increasing values of ![]() computed by the IQC-tools. This yields the results shown in the following figure. As can be seen, the IQC-analysis produces roughly the same worst-case
computed by the IQC-tools. This yields the results shown in the following figure. As can be seen, the IQC-analysis produces roughly the same worst-case ![]() -norms for the two considered relaxation schemes.
-norms for the two considered relaxation schemes.
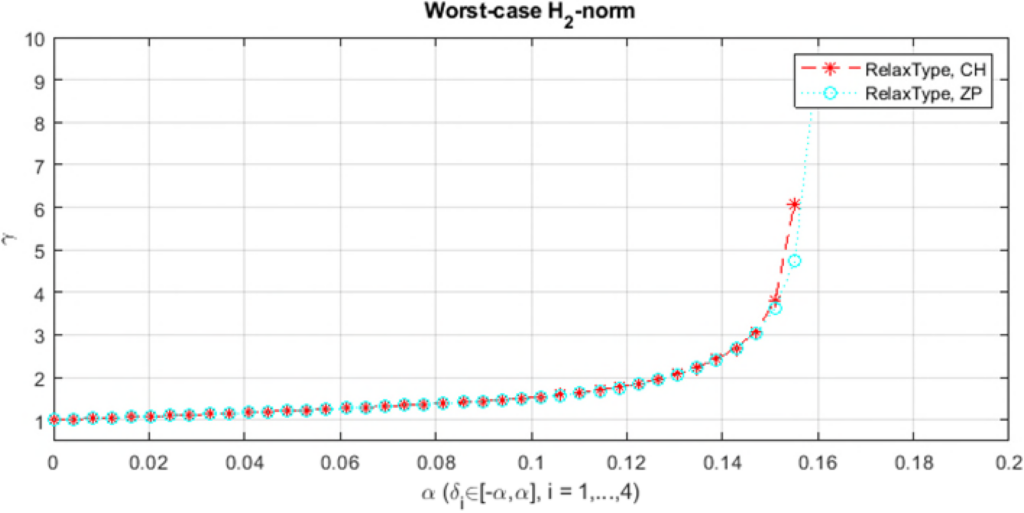
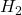 -norm for increasing values of
-norm for increasing values of 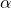 and different relaxation schemes
and different relaxation schemes