udel: Uncertain delay

The class udel is defined by diagonally repeated delay uncertainties of the form:

Type 1: $\Delta_{del1}=(e^{-s\tau}-1)I_{nr}$
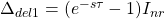
Type 2: $\Delta_{del2}=\frac{1}{s}(e^{-s\tau}-1)I_{nr}$

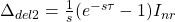
Here

$s$ is the Laplace operator
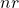$nr$ is the number of repetitions
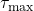$\tau\in[0,\tau_\mathrm{max}]$ with $\tau_\mathrm{max}$ being the maximum delay time.

The udel class can be defined by

$\Delta_\mathrm{del}=udel('name')$
$\Delta_\mathrm{del}=udel('name',varargin)$

Just specifying $\Delta_\mathrm{del}=udel('name')$ defines an LTI diagonally repeated delay uncertainty of Type 1, which has a maximum delay of $\tau_\mathrm{max}=1$ second and which is repeated once.

Specifying and/or changing properties proceeds as summarized in the following two tables for properties related to the uncertainty and to IQC-multiplier respectively.

Property	Description
DelayType	Specify the type of delay operator (i.e., Type 1 or Type 2) (Default = 1).
DelayTime	Specify the maximum time delay $\tau_\mathrm{max}$ for $\tau$ (default = 1).
NumberOfRepetitions	Specify the number of repetitions of the uncertainty (default = 1).
InputChannel/ OutputChannel	Specify which input and output channels of the uncertain plant are affected by $\Delta_\mathrm{udel}$ . The channels should be specified as: $\begin{array}{c} InputChannel=\left[ \! \! \! \begin{array}{ccc}C_{x}^{in}&\cdots&C_{y}^{in}\end{array} \! \! \! \right]\\OutputChannel=\left[ \! \! \! \begin{array}{ccc}C_{v}^{in}&\cdots&C_{w}^{in}\end{array} \! \! \! \right] \end{array}$ Here the order of the channels is not relevant, while $C_{m}^{in}$ , $C_{n}^{out}$ respectively denote the $m^{th}$ and $n^{th}$ in- and output channel of the uncertain plant $M$ .

Uncertainty characteristics

M(\infty)=0 — Multiplier characteristics

Note: See Section 5.5 of [1] for the details on the mathematical derivation of the IQC-multiplier.

Property	Description
BasisFunctionType	Specify the type of basis function to be used in the multiplier (default = 1). See link for further details.
Length	Specify the length of the basis function (default = 1). See link for further details.
PoleLocation	Specify the pole location of the basis function (default = -1). See link for further details.
AddIQC	Specify whether to add an additional LMI constraint for obtaining potentially improved results at the cost of more computational complexity. Note: The default value is ‘yes’.
MstrictlyProp	Specify whether the part of the plant that is seem by the uncertainty satisfies $M(\infty)=0$ . If so, one of the LMI constraints on the IQC (see previous property) can be dropped, allowing for more freedom in the optimization problem. Note 1: The default value is ‘no’. Note 2: This test is automatically turned to ‘yes’ in the IQC analysis if indeed $M(\infty)=0$ .
SampleTime	Specify the sample time (default = 0).
PrimalDual	Specify whether the multiplier should be a primal/dual parametrization (default = ‘Primal’). – Primal multipliers: ‘Primal’ – Dual multipliers: ‘Dual’ Note: For a standard IQC-analysis, all multipliers must be primal ones.