The class ultis is defined by LTI diagonally repeated parametric uncertainties of the form:
![Rendered by QuickLaTeX.com \[\Delta_\mathrm{ultis}=\left(\begin{array}{cccc}\delta_1I_{n_1}&0&\cdots & 0\\0 & \ddots & \ddots & \vdots\\ \vdots & \ddots & \ddots & 0\\0 & \cdots & 0 & \delta_NI_{n_N} \end{array}\right).\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-87ec45cf15030ef91ca7bbbdf1301d94_l3.png?media=1702023987)
 ,
, 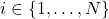 .
. is star convex (i.e.,
is star convex (i.e., ![Rendered by QuickLaTeX.com [0,1]\mathbf{S}\subset\mathbf{S}](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-bca69e974183d50c37cdb8e9c8db0fa8_l3.png?media=1702023987) )
)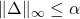
Note: In case the length of the basis function (i.e. one of the properties to be specified for this class) is 1, the class generalizes to the class of LTV diagonally repeated parametric uncertainties that can vary arbitrarily fast.
The ultis class can be defined by
Just specifying ![]() defines an LTI parametric uncertainty
defines an LTI parametric uncertainty ![]() of dimension
of dimension ![]() , which is repeated once and which satisfies
, which is repeated once and which satisfies ![]() .
.
Specifying and/or changing properties proceeds as summarized in the following two tables for properties related to the uncertainty and to IQC-multiplier respectively.
| Property | Description |
| NumberOfRepetitions | Specify the number of repetitions of the uncertainty (default = 1). Note: In case of more than one uncertainty, one needs to specify the number of repetitions as |
| Bounds | Specify the domain on which the uncertainty is defined (default = |
| Polytope | Alternatively, instead of using the option Bound one can specify the option Polytope: Note: It is always assumed that the 0 is contained in the set. |
| InputChannel/ OutputChannel | Specify which input and output channels of the uncertain plant are affected by Here the order of the channels is not relevant, while |
| Property | Description |
| BasisFunctionType | Specify the type of basis function to be used in the multiplier (default = 1). See link for further details. |
| Length | Specify the length of the basis function (default = 1). Note: In case of multiple diagonally repeated uncertainties, one can specify one common length, or a different one for each |
| PoleLocation | Specify the pole location of the basis function (default = -1). Note: In case of multiple diagonally repeated uncertainties, one can specify one common pole-location, or a different one for each |
| SampleTime | Specify the sample time (default = 0). |
| RelaxationType | Specify the relaxation type. Options are (default = ‘DG’): – DG-scalings: ‘DG’ – Convex hull relaxation: ‘CH’ – Partial convexity: ‘PC’ – Zeroth order Polya relaxation: ‘ZP’ |
| RelaxationProp | Specify the relaxation constraint type. Options are (default = ‘S’) – Static relaxation constraints: ‘S’ – Dynamic relaxation constraints: ‘D’ |
| PrimalDual | Specify whether the multiplier should be a primal/dual parametrization (default = ‘Primal’). – Primal multipliers: ‘Primal’ – Dual multipliers: ‘Dual’ Note: For a standard IQC-analysis, all multipliers must be primal ones. |
Note: See Section 5.3 of [1] for the details on the mathematical derivation of the IQC-multiplier.

![Rendered by QuickLaTeX.com \[\left[\begin{array}{ccc}\delta_1^{p_1}&\cdots& \delta_N^{p_1}\\\vdots& \cdots& \vdots\\ \delta_1^{p_M}&\cdots& \delta_N^{p_M}\end{array}\right]\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-c94f664a9a788e60afa2668be6b9a230_l3.png?media=1702023987)
![Rendered by QuickLaTeX.com \[ \begin{array}{c}InputChannel= \\ =\left\{\!\!\!\begin{array}{ccc}row_{in,1}\!\!\!&\cdots\!\!\!& row_{in,N} \end{array}\!\!\!\right\}\\OutputChannel =\\ =\left\{\!\!\!\begin{array}{ccc} row_{out,1}\!\!\!\!&\cdots\!\!\!\!&row_{ out ,N} \end{array}\!\!\!\right\}\end{array} \]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-5aa5ad0a15bad37b490b1f48ed0c5c01_l3.png?media=1702023987)