ultv_rb: LTV rate-bounded parametric uncertainties

The class ultv_rb is defined by LTV rate-bounded parametric uncertainties of the form:

$\left(\begin{array}{ccc}\delta_1I_{nr_1}&\cdots& 0\\\vdots&\ddots& \vdots\\0&\cdots& \delta_NI_{nr_N}\end{array}\right) .$

Here

$\delta_i\in\mathbf{\delta}_i$ , $i\in\{1,\ldots,N\}$ .
$\mathbf{\delta}_i=\left\{\delta_i(\cdot)\in C^1([0,\infty),\mathbb{R}):(\delta_i(t),\dot{\delta}_i(t))\in\Lambda\forall t\geq0\right\}$
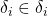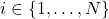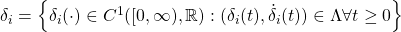
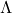$\Lambda$ is assumed to be star convex: $[0,1]\Lambda\subset\Lambda$ .

The ultv_rb class can be defined by

$\Delta_\mathrm{ultv\_ rm}=ultv\_ rm('name')$
$\Delta_\mathrm{ultv\_ rm}=ultv\_ rm('name',varargin)$

Just specifying $\Delta_\mathrm{ultv\_ rm}=ultv\_ rm('name')$ defines a rate-bounded LTV parametric uncertainty $\delta$ with $\delta\in[-1,1]$ and $\dot{\delta}\in[-1,1]$ , which is repeated once.

Specifying and/or changing properties proceeds as summarized in the following two tables for properties related to the uncertainty and to IQC-multiplier respectively.

[nr_1,\ldots,nr_N] — Uncertainty characteristics

Property	Description
BasisFunctionType	Specify the type of basis function to be used in the multiplier (default = 1). See link for further details.
Length	Specify the length of the basis function (default = 1). Note: In case of multiple diagonally repeated uncertainties, one can specify one common length, or a different one for each $\delta_i$ respectively as $l$ or $[l_1,l_2,\ldots]$ . See link for further details.
PoleLocation	Specify the pole location of the basis function (default = -1). Note: In case of multiple diagonally repeated uncertainties, one can specify one common pole-location, or a different one for each $\delta_i$ respectively as $pl$ or $[pl_1,pl_2,\ldots]$ . See link for further details.
SampleTime	Specify the sample time (default = 0).
RelaxationType	Specify the relaxation type. Options are (default = ‘DG’): – DG-scalings: ‘DG’ – Convex hull relaxation: ‘CH’ – Partial convexity: ‘PC’ – Zeroth order Polya relaxation: ‘ZP’
RelaxationProp	Specify the relaxation constraint type. Options are (default = ‘S’) – Static relaxation constraints: ‘S’ – Dynamic relaxation constraints: ‘D’
PrimalDual	Specify whether the multiplier should be a primal/dual parametrization (default = ‘Primal’). – Primal multipliers: ‘Primal’ – Dual multipliers: ‘Dual’ Note: For a standard IQC-analysis, all multipliers must be primal ones.

Multiplier characteristics

Note: See Section 5.4 of [1] for the details on the mathematical derivation of the IQC-multiplier.

Property	Description
NumberOfRepetitions	Specify the number of repetitions of the uncertainty (default = 1). Note: In case of more than one uncertainty, one needs to specify the number of repetitions as $[nr_1,\ldots,nr_N]$ .
Bounds	Specify the domain on which the uncertainty is defined (default = $\left[-1;1\right]$ ). $\left[\begin{array}{ccc}-\delta_1&\cdots&-\delta_N\\\delta_1&\cdots&\delta_N\end{array}\right]$
RateBounds	Specify the domain on which the uncertainty is rate-bounded (default = $\left[-1;1\right]$ ). $\left[\begin{array}{ccc}-\dot{\delta}_1&\cdots&- \dot{\delta} _N\\ \dot{\delta} _1&\cdots& \dot{\delta} _N\end{array}\right]$
Polytope	Alternatively, instead of using the option Bounds/RateBounds one can specify the option Polytope: $\left[\begin{array}{ccccc}\delta_1^{p_1}&\dot{\delta}_1^{p_1}& \cdots& \delta_N^{p_1} & \dot{\delta}_N^{p_1} \\ \vdots& \vdots& \cdots& \vdots& \vdots\\ \delta_1^{p_M}&\dot{\delta}_1^{p_M}&\cdots& \delta_N^{p_M} & \dot{\delta}_N^{p_M} \end{array}\right]$ Note: It is always assumed that the 0 is contained in the set.
InputChannel/ OutputChannel	Specify which input and output channels of the uncertain plant are affected by $\Delta_\mathrm{ultv\_ rm}$ . For each $\delta_i$ , the channels should be specified as: $\begin{array}{c} row_{in,i}=\left[\begin{array}{ccc}C_{x_i}^{in}&\cdots&C_{y_i}^{in}\end{array}\right]\\row_{out,i}=\left[\begin{array}{ccc}C_{v_i}^{in}&\cdots&C_{w_i}^{in}\end{array}\right] \end{array}$ Here the order of the channels is not relevant, while $C_{m_i}^{in}$ , $C_{n_i}^{out}$ respectively denote the $m^{th}$ and $n^{th}$ in- and output channel of the uncertain plant $M$ . Note here thatthe row length of $row_{in,i}$ and $row_{out,i}$ equals the number of repetitions of $\delta_i$ . The option InputChannel/ OutputChannel should then be specified as a cell: $\begin{array}{c}InputChannel= \\ =\left\{\!\!\!\begin{array}{ccc}row_{in,1}\!\!\!&\cdots\!\!\!& row_{in,N} \end{array}\!\!\!\right\}\\OutputChannel =\\ =\left\{\!\!\!\begin{array}{ccc} row_{out,1}\!\!\!\!&\cdots\!\!\!\!&row_{ out ,N} \end{array}\!\!\!\right\}\end{array}$